Infinite Limits for MATH 122
Exam Relevance for MATH 122
Infinite limits appear occasionally in MATH 122 for asymptotic behavior of functions.
What is an Infinite Limit?
An infinite limit happens when a function grows without bound (gets infinitely large or infinitely negative) as $x$ approaches some value.
Notation:
- $\displaystyle\lim_{x \to a} f(x) = \infty$ means $f(x)$ grows toward positive infinity
- $\displaystyle\lim_{x \to a} f(x) = -\infty$ means $f(x)$ grows toward negative infinity
Important: Technically, the limit "does not exist" when it's $\pm\infty$, because infinity isn't a real number. But we write $= \infty$ to describe the behavior.
In this graph, we see the function $f(x) = \frac{1}{x}$. Notice how the function shoots up toward $+\infty$ as $x$ approaches $0$ from the right, and plunges down toward $-\infty$ as $x$ approaches $0$ from the left. The y-axis ($x = 0$) is a vertical asymptote.
Vertical Asymptotes
When $\displaystyle\lim_{x \to a} f(x) = \pm\infty$, the line $x = a$ is called a vertical asymptote.
The graph shoots up or down toward this vertical line but never actually touches it.
When Do Infinite Limits Happen?
Infinite limits occur when:
- The denominator approaches 0
- The numerator approaches a non-zero number
$$\frac{\text{non-zero}}{\text{something approaching } 0} \to \pm\infty$$
How to Determine the Sign ($+\infty$ or $-\infty$)
The key question: What's the sign of the function near $x = a$?
Check:
- Is the numerator positive or negative near $a$?
- Is the denominator approaching $0^+$ (small positive) or $0^-$ (small negative)?
$$\frac{(+)}{(0^+)} = +\infty \qquad \frac{(+)}{(0^-)} = -\infty$$ $$\frac{(-)}{(0^+)} = -\infty \qquad \frac{(-)}{(0^-)} = +\infty$$
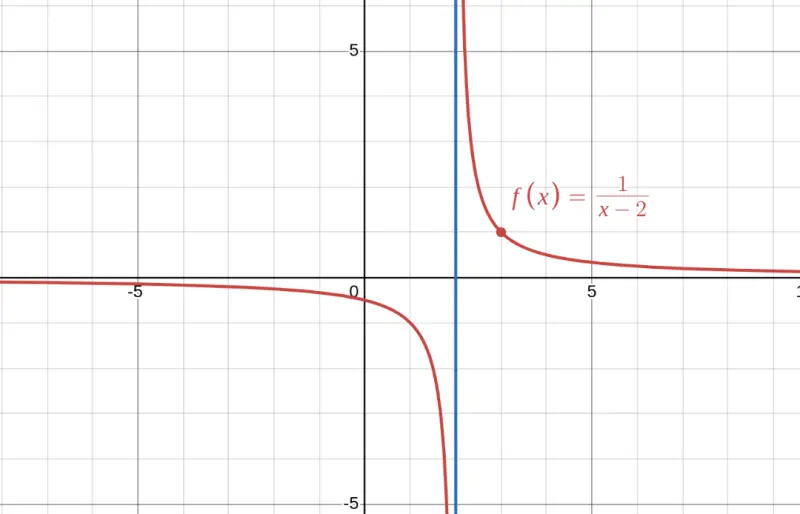
In this graph, we see $f(x) = \frac{1}{x-2}$ with a vertical asymptote at $x = 2$. From the left ($x \to 2^-$), the function goes to $-\infty$. From the right ($x \to 2^+$), it goes to $+\infty$. This is why the two-sided limit DNE.
Problem: Find $\displaystyle\lim_{x \to 2} \frac{1}{(x-2)^2}$
Step 1: What happens to the denominator?
As $x \to 2$: $(x-2)^2 \to 0$
Step 2: What's the sign?
$(x-2)^2$ is always positive (squared term), so the denominator approaches $0^+$.
Step 3: Combine: $$\frac{1}{(0^+)} = +\infty$$
$$\boxed{\lim_{x \to 2} \frac{1}{(x-2)^2} = \infty}$$
Problem: Find $\displaystyle\lim_{x \to 3^+} \frac{2}{x-3}$ and $\displaystyle\lim_{x \to 3^-} \frac{2}{x-3}$
From the right ($x \to 3^+$, so $x > 3$):
- Numerator: $2$ (positive)
- Denominator: $x - 3 > 0$ and $\to 0^+$ $$\frac{2}{0^+} = \boxed{+\infty}$$
From the left ($x \to 3^-$, so $x < 3$):
- Numerator: $2$ (positive)
- Denominator: $x - 3 < 0$ and $\to 0^-$ $$\frac{2}{0^-} = \boxed{-\infty}$$
Since the one-sided limits are different, $\displaystyle\lim_{x \to 3} \frac{2}{x-3}$ DNE.
Problem: Find all vertical asymptotes of $f(x) = \frac{x+1}{x^2-4}$
Step 1: Find where the denominator equals zero: $$x^2 - 4 = 0$$ $$(x-2)(x+2) = 0$$ $$x = 2 \text{ or } x = -2$$
Step 2: Check that the numerator is NOT zero at these points:
- At $x = 2$: numerator $= 2 + 1 = 3 \neq 0$ ✓
- At $x = -2$: numerator $= -2 + 1 = -1 \neq 0$ ✓
Step 3: Vertical asymptotes at $\boxed{x = 2}$ and $\boxed{x = -2}$
Problem: Analyze $f(x) = \frac{x^2-4}{x-2}$
Step 1: Factor: $$\frac{x^2-4}{x-2} = \frac{(x-2)(x+2)}{x-2} = x + 2 \quad (x \neq 2)$$
Step 2: At $x = 2$, both numerator and denominator equal zero.
After canceling, we get $x + 2$, which is defined at $x = 2$.
This means $x = 2$ is a hole (removable discontinuity), NOT a vertical asymptote!
$$\lim_{x \to 2} \frac{x^2-4}{x-2} = 2 + 2 = \boxed{4}$$

In this graph, compare two functions: $f(x) = \frac{1}{x-2}$ (which has a vertical asymptote at $x=2$) and $g(x) = \frac{x^2-4}{x-2}$ (which simplifies to the line $y = x+2$ with a hole at $(2, 4)$). Notice the dramatic difference — one blows up to infinity, the other just has a single missing point!
Key Distinction
| Situation | What Happens | Result |
|---|---|---|
| $\frac{0}{0}$ | Cancel common factor | Usually a hole (finite limit) |
| $\frac{\text{non-zero}}{0}$ | Can't cancel | Vertical asymptote ($\pm\infty$) |
Common Mistakes and Misunderstandings
❌ Mistake: Writing $\lim = \infty$ means the limit "exists"
Wrong thinking: "The limit equals infinity, so it exists."
Why it's wrong: Infinity is not a real number. When we write $\lim_{x \to a} f(x) = \infty$, we're describing behavior, not stating an actual value. The limit technically does not exist (DNE).
Correct: Say "the limit is infinite" or "the limit does not exist (it goes to infinity)."
❌ Mistake: Confusing $\frac{0}{0}$ with $\frac{\text{non-zero}}{0}$
Wrong: "The denominator is zero, so the limit is $\infty$."
Why it's wrong:
- $\frac{0}{0}$ is indeterminate — you need to simplify first (often gives a finite limit or a hole)
- $\frac{\text{non-zero}}{0}$ gives $\pm\infty$ (vertical asymptote)
Correct: Always check BOTH the numerator AND denominator before concluding.
❌ Mistake: Forgetting to check one-sided limits
Wrong: $\displaystyle\lim_{x \to 2} \frac{1}{x-2} = \infty$
Why it's wrong: From the left, it goes to $-\infty$. From the right, it goes to $+\infty$. Since they disagree, the two-sided limit DNE (not just "equals infinity").
Correct: $$\lim_{x \to 2^-} \frac{1}{x-2} = -\infty, \quad \lim_{x \to 2^+} \frac{1}{x-2} = +\infty$$ $$\therefore \lim_{x \to 2} \frac{1}{x-2} \text{ DNE}$$
❌ Mistake: Assuming every zero in the denominator is a vertical asymptote
Wrong: "$f(x) = \frac{x-3}{x-3}$ has a vertical asymptote at $x = 3$."
Why it's wrong: After canceling, $f(x) = 1$ for all $x \neq 3$. There's a hole at $x = 3$, not an asymptote.
Correct: Only $\frac{\text{non-zero}}{0}$ creates a vertical asymptote. If both are zero, factor and simplify first.
❌ Mistake: Getting the sign wrong on one-sided limits
Wrong: $\displaystyle\lim_{x \to 5^-} \frac{3}{x-5} = +\infty$
Why it's wrong: When $x < 5$, we have $x - 5 < 0$, so the denominator is negative. $$\frac{(+)}{(0^-)} = -\infty$$
Correct: $\displaystyle\lim_{x \to 5^-} \frac{3}{x-5} = -\infty$
Tip: Plug in a test value! Try $x = 4.9$: $\frac{3}{4.9-5} = \frac{3}{-0.1} = -30$ (negative!)
This skill is taught in the following courses. Create an account to access practice exercises and full course materials.